Geogebra
¿QUÉ ES GEOGEBRA?
Geogebra es un Programa Dinámico para la Enseñanza y Aprendizaje de las Matemáticas para educación en todos sus niveles. Combina dinámicamente, geometría, álgebra , análisis y estadística en un único conjunto tan sencillo a nivel operativo como potente.
Ofrece representaciones diversas de los objetos desde cada una de sus posibles perspectivas: vistas gráficas, algebraicas, estadísticas y de organización en tablas y planillas, y hojas de datos dinámicamente vinculadas.
Geogebra es en su origen la tesis de Markus Hohenwarter, con el objeto de crear una calculadora de uso libre para trabajar el Álgebra y la Geometría.
Fue un proyecto que se inició en el 2001 en un curso de Matemática en la Universidad de Salzburgo (Austria). Actualmente, Geogebra continúa su desarrollo en la Universidad de Boca Raton, Florida Atlantic University (USA). Pero no tenemos que olvidar que GeoGebra está diseñado con mentalidad colaborativa. Desde la página oficial disponemos de acceso a ayudas, recursos, foros y wikis que usuarios de todo el mundo mantienen en constante renovación.
¿POR QUÉ ES INTERESANTE UTILIZAR GEOGEBRA?
Además de la gratuidad y la facilidad de aprendizaje, la característica más destacable de GeoGebra es la doble percepción de los objetos, ya que cada objeto tiene dos representaciones, una en la Vista Gráfica (Geometría) y otra en la Vista Algebraica (Álgebra). De esta forma, se establece una permanente conexión entre los símbolos algebraicos y las gráficas geométricas.• Todos los objetos que vayamos incorporando en la zona gráfica le corresponderá una expresión en la ventana algebraica y viceversa.
- Posee características propias de los programas de Geometría Dinámica (DGS) pero también de los programas de Cálculo Simbólico (CAS). Incorpora su propia Hoja de Cálculo, un sistema de distribución de los objetos por capas y la posibilidad de animar manual o automáticamente los objetos.
- Facilidad para crear una página web dinámica a partir de la construcción creada con Geogebra, sin más que seleccionar la opción correspondiente en los menus que ofrece..
- Permite abordar la geometría y otros aspectos de las matemáticas, a través de la experimentación y la manipulación de distintos elementos, facilitando la realización de construcciones para deducir resultados y propiedades a partir de la observación directa.
- Es gratuito y de código abierto (GNU GPL).
- Está disponible en español, incluido el manual de ayuda.
- Presenta foros en varios idiomas, el castellano entre ellos.
- Ofrece una wiki en donde compartir las propias realizaciones con los demás.
- Usa la multiplataforma de Java, lo que garantiza su portabilidad a sistemas de Windows, Linux, Solaris o MacOS X.
FORMAS DE TRABAJAR CON GEOGEBRA
GeoGebra permite abordar la geometría desde una forma dinámica e interactiva que ayuda a los estudiantes a visualizar contenidos matemáticos que son más complicados de afrontar desde un dibujo estático.
También permite realizar construcciones de manera fácil y rápida, con un trazado exacto y real, que además, revelarán las relaciones existentes entre la figura construida; también permitirá la transformación dinámica de los objetos que la componen.
Debido a estas dos características el profesorado y el alumnado pueden acercarse a GeoGebra de varias maneras, no excluyentes entre sí pero que a menudo están relacionadas con el nivel de capacitación que se tenga del programa.
Herramienta del profesor
Se pueden utilizar construcciones ya creadas por otras personas o las realizadas por nosotros mismos para:
- Crear materiales educativos estáticos (imágenes, protocolos de construcción) o dinámicos (demostraciones dinámicas locales, applets en páginas web), que sirvan de apoyo a las explicaciones de la materia.
- Crear actividades para que los alumn@s manipulen dichas construcciones y así deduzcan relaciones, propiedades y resultados a partir de la observación directa.
Herramienta del estudiante:
- Manipular construcciones realizadas por otras personas y deducir relaciones, resultados y propiedades de los objetos que intervienen.
- Para realizar construcciones desde cero, ya sean dirigidas o abiertas, de resolución o de investigación.
NIVELES DE CERTIFICACIÓN
El Instituto Internacional de Geogebra establece diferentes niveles de certificación para sus usuarios.
- Certificado de USUARIO
- Certificado de EXPERTO
- Certificado de FORMADOR
Para cada uno de los niveles se establecen una serie de conocimientos y capacidades sobre el uso de Geogebra que deberán acreditarse para alcanzar la correspondiente certificación.
Estos conocimientos y capacidades comprenderan tres ámbitos de actuación:
- Conocimiento técnico de Geogebra.
- Aplicación de Geogebra en la Enseñanza y Aprendizaje.
- Papel en la Comunidad de Usuarios de Geogebra
Certificado de Usuario
Los usuarios que tienen este nivel se caracterizan por tener la capacidad de crear construcciones dinámicas sencillas y utilizar con éxito materiales en procesos de enseñanza-aprendizaje.
Los candidatos a obtener el certificado de Usuario tendrán que demostrar los conocimientos y capacidades siguientes:
Conocimiento técnico de GeoGebra:
- Familiaridad con las ventanas disponibles, las herramientas geométricas y el uso de comandos básicos.
- Capacidad para cambiar las propiedades de los objetos con el objetivo de crear construcciones atractivas.
- Utilización de GeoGebra para crear archivos ggb, exportación como imagen y como página web.
- Capacidad para buscar información el documento de Ayuda.
La aplicación a la enseñanza y aprendizaje:
- Conocimiento de las capacidades dinámicas de GeoGebra y su potencial de representación en diferentes formatos.
- Uso de GeoGebra como herramienta de representación y de demostración.
- Selección de materiales publicados en Internet.
El papel en la comunidad de usuarios de GeoGebra:
- Capacidad para plantear preguntas en el foro de usuarios de GeoGebra.
Certificado de Experto
Como características para este nivel se establecen que los usuarios expertos deben ser capaces de realizar construcciones con GeoGebra que incorporen distintos elementos, no solo geométricos sino también algebraicos, que permitan animaciones, conocer los procesos para exportar archivos y, que sean capaces de analizar y evaluar construcciones realizadas por otros usuarios.
Los usuarios que tienen este nivel se caracterizan por elaborar y compartir materiales didácticos realizados con GeoGebra y realizar tareas de apoyo a otros usuarios de la comunidad GeoGebra.
Los candidatos a obtener el certificado de Experto tendrán que demostrar los conocimientos y capacidades siguientes.
Conocimiento técnico de GeoGebra:
- Familiaridad con el uso de expresiones algebraicas y comandos.
- Familiaridad con el uso de características avanzadas.
- Uso del protocolo de construcción y otras estrategias para saber como se creó una construcción.
- Capacidad para crear herramientas definidas por el usuario. Capacidad para personal el entorno de trabajo.
- Familiaridad con las opciones avanzadas.
La aplicación a la enseñanza y aprendizaje:
- Uso de GeoGebra como herramienta para realización de construcciones.
- Uso de GeoGebra en el aprendizaje por descubrimiento y experimentación.
- Capacidad de adaptar construcciones existentes.
- Capacidad de introducir y guiar a otros usuarios en los primeros pasos con GeoGebra.
El papel en la comunidad de usuarios de GeoGebra:
- Capacidad para responder a las preguntas en el foro de usuarios y proporcionar orientación y apoyo.
- Capacidad para crear y compartir materiales educativos innovadores dentro de la comunidad GeoGebra.
- Participación activa en actividades con otros usuarios con la finalidad de colaborar y intercambiar conocimiento y experiencias.
- Capacidad para dar talleres para principiantes con el fin de introducirles en GeoGebra.
Certificado de Formador
Para acceder a este nivel se tendrá que participar como ponente en actividades de formación sobre GeoGebra, formar parte de grupos de trabajo cuyo objetivo sea la formación o la elaboración de materiales o de unidades didácticas, así como participar de manera activa en el proyecto GeoGebra o colaborando con un instituto local reconocido por el Instituto Internacional de GeoGebra.
Los candidatos a obtener el certificado de Formador tendrán que demostrar los conocimientos y capacidades siguientes:
Conocimiento técnico de GeoGebra:
- Familiaridad con la mayoría de características de GeoGebra y larga experiencia con el software.
- Conocimiento sobre dónde obtener información adicional a cerca del uso de características desconocidas y nuevas del software.
- Conocimiento sobre las diferentes maneras de instalar GeoGebra en un equipo.
- Familiaridad con características muy avanzadas de GeoGebra.
La aplicación a la enseñanza y aprendizaje:
- Experiencia en el uso de GeoGebra en diversos situaciones de enseñanza-aprendizaje, al menos un año.
- Habilidad para utilizar y adaptar materiales para distingos grupos de participantes en un taller o curso.
El papel en la comunidad de usuarios de GeoGebra:
- Colaboración con un instinto de GeoGebra local.
- Capacidad para dar talleres para principiantes y avanzados así como impartir conferencias y participar en congresos.
- Capacidad para hacer contribuciones en plataformas on-line que fomentan la colaboración entre los miembros de la comunidad GeoGebra.
- Capacidad para hacer investigaciones, para publicar artículos y para compartir experiencias con la comunidad GeoGebra.
https://sites.google.com/site/geogebra1112/caracteristicas-de-geogebra
Vistas y apariencias
GeoGebra ofrece diversas vistas para los objetos matemáticos.
 Vista Algebraica |  Vista Gráfica |  Vista gráfica 3D |
 Vista CAS |  Hoja de Cálculo |  Calculadora de Probabilidades |
Cada vista presenta su propia barra de herramientas con un repertorio de herramientas y comandos, así como operadores y funciones que permiten crear construcciones dinámicas con diferentes representaciones de los objetos matemáticos.
Según los contenidos matemáticos con los que se desee trabajar, se puede seleccionar una de las Apariencias ofrecidas. Cada apariencia despliega las vistas y otras componentes de la interfaz que son relevantes para el contenido matemático de interés.
Parámetros y su función en las Funciones
En este tutorial, se va a indagar sobre el efecto de los parámetros de diversas funciones, empleando los deslizadores de GeoGebra para modificarlos y registrar correlatos en las representaciones gráfica.
Preparativos
En el Menú Apariencias, es preciso seleccionar la adecuada y:
- dejar activa la barra de estilo
- exponer los ejes de coordenadas.
Reconocer las herramientas que van a emplearse:
 | Deslizador |
| Recta: y = m x + b | |
 | Segmento |
| Interseca[recta, Eje Y] | |
 | Intersección |
 | Pendiente |
 | Objeto (in)visible |
 | Elije y Mueve |
https://wiki.geogebra.org/es/Manual
Esta es la pagina donde puedes consultar la pagina de geogebra donde hay actividades donde puedes fomentar todo lo que has aprendido o para conocer herramientas por el cual es que se utilizan para poder entender las dinámicas que se te dan como por ejemplo poder hacer rectas o triángulos para poder medir los ángulos que quieres ademas de hacer cálculos por el cual tu te puedes enseñar a utilizar las herramientas que se te muestran, a continuación les dejo la pagina de geogebra para poder interactuar con las herramientas:
https://www.geogebra.org/?lang=es
Te vamos a enseñar como tienes que utilizar geogebra con un ejemplo:
Te vamos a enseñar como tienes que utilizar geogebra con un ejemplo:
El desafío es encontrar un triángulo tri que se ajuste a los rastros que quedaron del que se perdió que son, solo los que se listan:
- algunos puntos por los que pasaba la circunferencia que lo circunscribía
- el de intersección de sus alturas
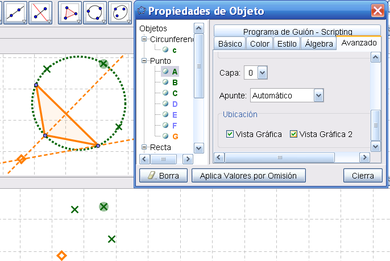
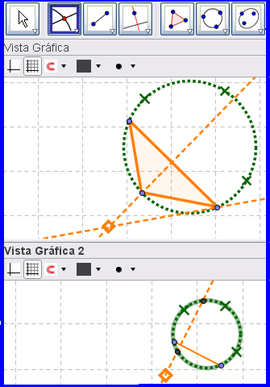
Para encarar esta propuesta, convendrá empezar por trazar, en la Vista Gráfica 1, la figura de análisis haciendo de cuenta que tenemos el caso resuelto para considerarla en retrospectiva. Cuando la completemos, en la Vista Gráfica 2 permitimos que se hagan visibles, solo los tres puntos por los que pasa la circunferencia y el de intersección de las alturas. Es entonces que, en la Vista Gráfica 2, se procura trazar un triángulo tal que...
- los tres puntos correspondan a la circunferencia que lo circunscribe
- sus alturas se intersequen en el punto restante.
Empezando por construir el Triángulo que habrá de Perderse
Para construir, en la Vista Gráfica 1 lo descripto, se procede a...
- Con la
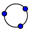Herramienta de Circunferencia por tres puntos, se traza la circunferencia que pasa por tres puntos distribuidos a gusto. - Con la
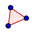Herramienta de Polígono, cuidando que los tres vértices que se seleccionen queden sobre la circunferencia recién trazada, se crea el triángulo que luego se renombrará como tri , uniendo uno a uno y cerrándolo con clic sobre el primero. - Con la
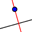Herramienta de Perpendicular, se traza las que pasan por uno y otro de los vértices de tri y son perpendiculares a sendos lados opuestos. - Con la
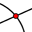Herramienta de Intersección, se establece el punto de intersección de las alturas. - En el Menú Vista se opta por hacer también visible la Vista Gráfica 2.
- Como se aprecia en la figura, en la pestaña Avanzado del Cuadro de Propiedades de los primeros tres puntos y del último, el de intersección de las alturas, se tilda la casilla de Vista Gráfica 2 para pasar a encarar el desafío en cuestión.
Tanteando y Explorando
Se pasa ahora al desafío mismo, que se desenvuelve en la Vista 2.
Reconstrucción Tanteada
Es posible encontrar múltiples estrategias de resolución por tanteos.
Por ejemplo, las que se corresponden con maniobras como las que se listan a continuación.
- Con la herramienta ya empleada, se traza una circunferencia que pase por los tres puntos por los que podría haber cruzado la que circunscribía al perdido tri
- Se traza un
segmento sobre la circunferencia como lado tentativo del triángulo a ajustar a los rastros del perdido tri. - Se traza ahora, la perpendicular que pasa por el punto que podría haber sido el de intersección de las alturas del perdido tri, al segmento recién trazado.
- Se determinan los puntos de intersección entre la circunferencia y la perpendicular recién trazada.
- Se traza un segmento entre uno de los extremos del primero que ha obrado las veces de sobre lado tentativo del triángulo y uno de los dos puntos de intersección.
- Se establece la perpendicular al nuevo segmento que pasa por el punto de intersección de las alturas.
- Se completa el triángulo en marcha uniendo ahora los tres vértices tentativos y se corrobora que existe una perpendicular al tercero de los lados que pasa por el punto de intersección de las alturas del perdido tri.
- Se
desplazan los dos primeros puntos para ver qué variedad de triángulos se obtiene, procurando establecer el que más se asemeje al modelo de la Vista Gráfica 1. - que hay más de una solución tanteada
- que son numerosos, acaso infinitos (pero no arbitrarios), los triángulos adecuados.
¡Todos comparten los elementos que el perdido tri dejó como rastro!
Esta bien interesante hechale ganas
ResponderBorrarNO POS MEAW :)
ResponderBorrar